Магический квадрат

Магический квадрат очень популярен среди любителей логических игр. Представляет собой таблицу, заполненную числами особым образом. Кроме того, сумма чисел одинакова во всех направлениях. Это значение называется константой. Существует множество вариантов таких головоломок разной степени сложности.

История и современное применение

Первые таблицы такого типа использовались в Древней Греции и Китае. Это подтверждают археологические находки. Арабы называли квадраты магическими, так как считали, что они обладают магическими свойствами и могут защитить от многих напастей.

Читайте также: Магия числа 26 — влияние на судьбу человека

В середине XVI века вопрос о том, как работает магический квадрат, заинтересовал математиков Европы. Они начали активно исследовать таинственные комбинации цифр. Ученые стремились вывести общие принципы построения квадратов и найти полный набор возможных вариантов.

В современной средней школе на уроках математики используются различные виды магических квадратов. Они способствуют развитию логического мышления и вызывают большой интерес у детей.

С ее помощью студенты учатся планировать свою работу и контролировать ее. В ячейки можно вводить не только отдельные числа, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Вы также можете решить эти виды числовых задач онлайн.

Квадрат нечётного порядка

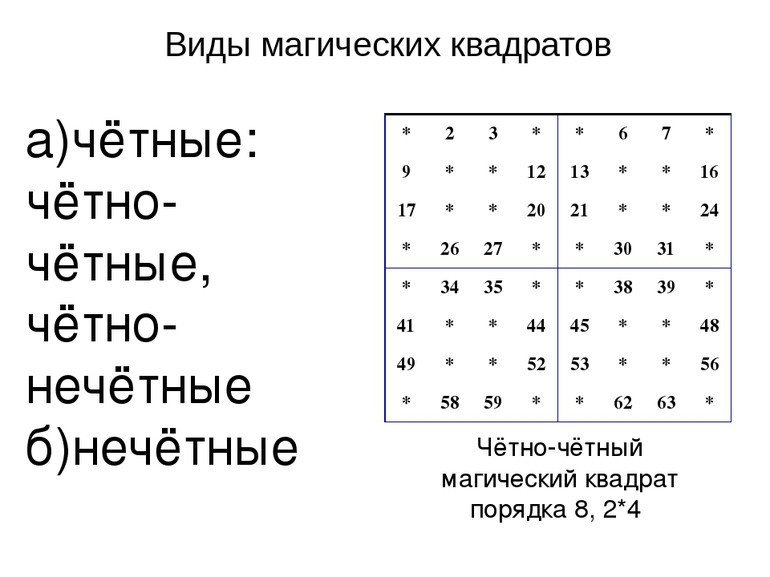
Среди простых магических квадратов в математике выделяют разновидности четного и нечетного порядка. Первая группа подразделяется на таблицы одинарной и двойной четности.

Первым шагом во всех случаях является определение магической константы. Делается это по специальной формуле [n*(n2+1)]/2. Понять принцип решения такой задачи можно на простейшем примере. Для этого строится таблица из 9 ячеек. Вы должны расставить числа от 1 до 9. Дополнительный алгоритм:

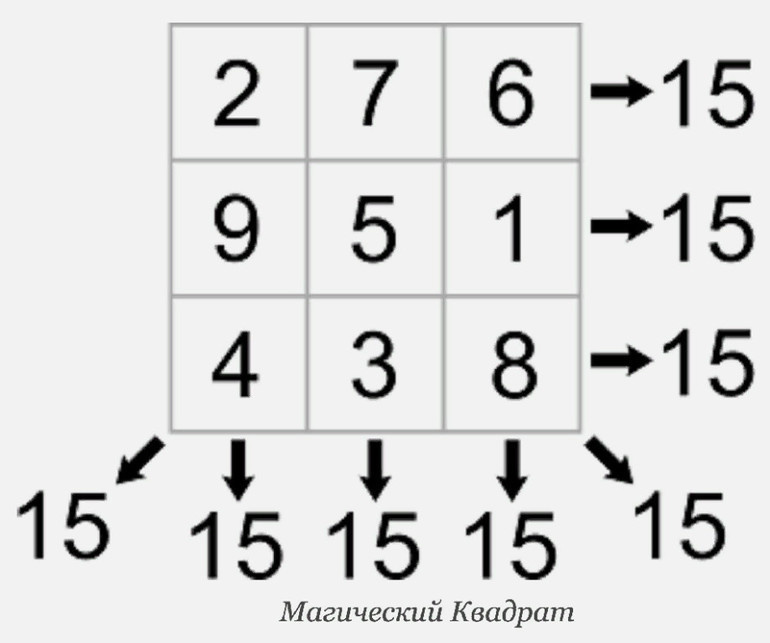
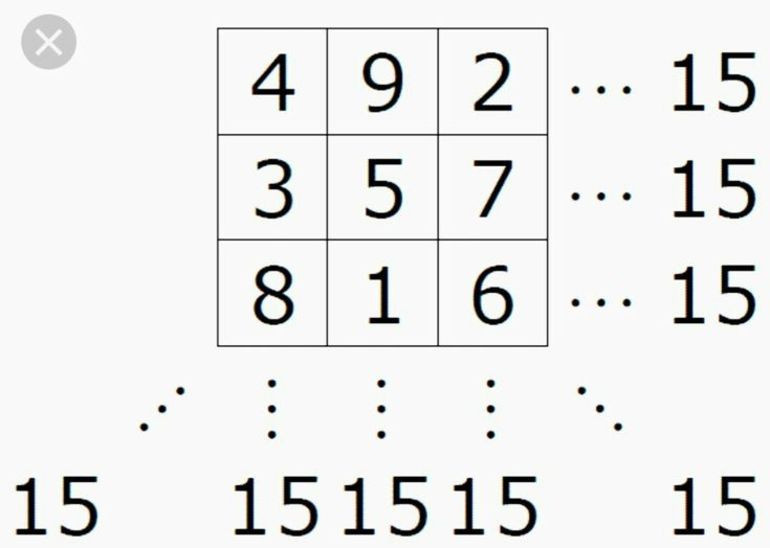
1. Рассчитывается сумма, которую нужно получить в каждой строке. Для этого используется формула: 3*(32+1)/2=3*10/2. Ответ будет номер 15.
2. Числа в ячейках расположены так, что в сумме они составляют 15 в каждой строке. Требуется изобретательность и воображение.
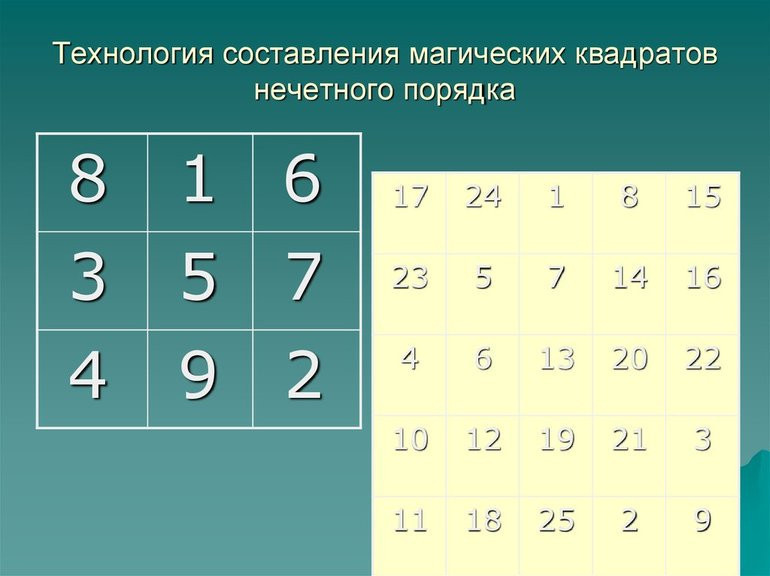
3. 1 вводится в среднюю ячейку верхней строки.
4. Каждое следующее число ставится по диагонали вверх вправо. Цифру 2 поставить нельзя, так как строк выше нет. Если вы мысленно добавите сверху еще один квадрат, цифра 2 окажется в правом нижнем углу. Таким образом, цифра 2 помещается в нижнюю правую ячейку.
5. По такому же принципу вводится цифра 3. Она попадает в среднюю ячейку слева.
6. Если нужная ячейка уже занята, следующий символ вводится ниже предыдущего. Так что 4 меньше 3.
7. Цифра 5 пишется по диагонали вправо и вверх, а 6 в правом верхнем углу.
8. Поскольку место числа 7 уже занято, оно подходит под число 6.
9. Восьмерка занимает место в левом нижнем углу.
10. Оставшаяся ячейка занята девятью.

Общий алгоритм выполнения задания: каждый следующий символ пишется вверх и вправо. Если клетки там нет, рисуется еще один воображаемый квадрат. Если ячейка занята, число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечетного порядка, даже самый сложный, с большим количеством клеток.

Читайте также: Значение цифры 0 в жизни человека

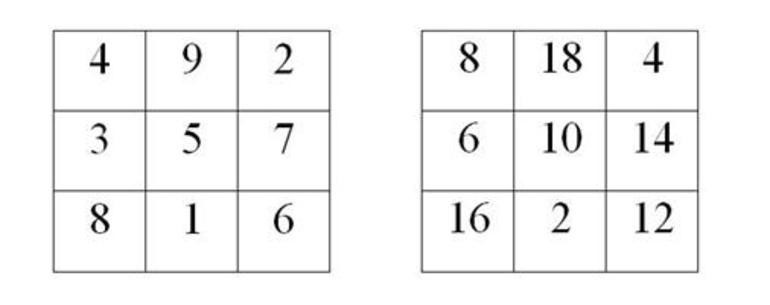
Одинарная чётность

Магические квадраты могут иметь порядок одинарной или двойной четности. Для каждого случая предусмотрена отдельная методика расчета. Для таблиц с одинарной четностью количество ячеек в строке или столбце уменьшается вдвое, но не делится на четыре. Наименьший квадрат, отвечающий этому требованию, — прямоугольник 6×6. Невозможно построить и заполнить фигуру 2х2.

Вычисление магической константы

Первый этап расчетов проводится по формуле [n*(n2+1)]/2, где символ n обозначает количество ячеек в ряду. Если взять в качестве примера квадрат 6х6, расчет будет выглядеть так: [6 х (36 + 1)]: 2 = (6 х 37): 2 = 222:2.

Магическая константа прямоугольника со стороной 6 клеток равна 111. Сумма чисел от 1 до 36 в каждом ряду и в разных направлениях должна равняться 111.

Рисунок разделен на 4 одинаковые части. В каждой будет по 9 ячеек (3х3). Каждая часть обозначается латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая. Если квадрат имеет другой размер, разделите n на 2, чтобы найти точный размер каждой из 4 частей.

Дальнейшие действия

Следующим шагом будет вписать ¼ всех чисел в каждую часть. Числа от 1 до 9 вводятся в квадранте А, от 10 до 18 в квадранте В, от 19 до 27 в части С и от 28 до 36 в части D.

Последовательность написания та же, что и при заполнении самого простого нечетного квадрата:

1. Минимальное число, которое начинает заполнять ячейки, всегда помещается в верхний ряд посередине. Для каждой части эта ячейка располагается отдельно.
2. Каждая часть заполняется как новый математический объект. Даже если в другом квадрате есть пустое место, оно в этих случаях игнорируется.

В блоках А и Г на данном этапе решения сумма по строкам и столбцам будет отличаться от константы. Чтобы исправить это, некоторые числа меняются местами друг с другом.

Алгоритм действий:

1. Он должен начинаться с крайней левой ячейки в верхнем ряду. Если фигура 6х6, то выделяется только первая верхняя строка части А. В нее следует вписать число 8. Если размер таблицы 10х10, выделить первые 2 ячейки верхней строки. Им 17 и 24 года.
2. Из выбранных ячеек формируется промежуточный квадрат. В таблице со строками и столбцами 6×6 она будет состоять из 1 ячейки. Условно обозначается как А1.
3. Если размер 10×10, то в верхней строке выбираются первые 2 ячейки. Вместе с ними выделяется еще 2 клетки, на второй строке получается поле из 4-х соседних друг с другом клеток.
4. В следующей строке пропускается первая ячейка, затем выбирается столько ячеек, сколько было в промежуточной таблице А1. Полученную цифру можно обозначить А2.
5. Таким же образом строится промежуточный квадрат A3.
6. Эти 3 промежуточные формы образуют выбранную область А.
7. Затем они перемещаются в квадрант D и образуют отдельную область D.

Числа, которые были вписаны в выбранные треугольники A и D, необходимо поменять местами. После этого сумма в каждой строке должна быть одинаковой. Он равен расчетной магической константе.

Двойной порядок

Если головоломка имеет двойной порядок четности, количество окон в каждой горизонтальной строке или вертикальном столбце должно делиться на 4. Минимальная фигура с этими свойствами будет таблицей 4×4.

Решение магических квадратов с двойной четностью следует тому же алгоритму, что и остальные. Первым шагом заполнения является вычисление магической константы. Используется та же формула, что и для расчета других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.

Промежуточные столы выделяются в каждом углу основного поля. Его размер должен быть равен n/4. Эти участки обозначают буквами A, B, C, D, располагая их против часовой стрелки. Размер промежуточных фигур зависит от размера исходного квадрата:

1. Если длина стороны 4 клетки, промежуточные зоны будут иметь 1 клетку.
2. В таблице 8×8 эти области включают 4 элемента (2×2).
3. В квадрате 12х12 можно выделить промежуточные фигуры размером 3х3.

Следующим шагом будет создание центрального среднего квадрата. Размер его стороны должен быть n/2. Эта фигура не должна перекрываться с периферийными, но в то же время соприкасаться с ними по углам.

Затем числа вписываются в квадрат слева направо. Их можно размещать только в свободных ячейках, входящих в состав промежуточных зон. Например, при заполнении таблицы 4х4 порядок действий будет следующим:

1. В первой строке сверху и первом столбце слева напишите 1. В верхней ячейке четвертого столбца напишите 4.
2. Цифры 6 и 7 располагаются в центре второй горизонтальной линии.
3. В четвертой строке напишите 13 слева и 16 справа.

По такому же принципу остальные ячейки заполняются цифрами. Цифры перечислены слева в порядке убывания. Если все сделано правильно, сумма всех чисел в любой строке будет одинаковой.