Обсудите, что любой вариант шестизначного множества этого и ему подобных пандиагональных квадратов 4 × 4, образующих непрерывную симметричную конфигурацию, равен целому числу: всего 51. Построена геометрическая фигура куб-в-кубе, обладающая свойствами «золотой симметрии» пандиагональных квадратов 4 × 4. Свойствами «золотой симметрии» обладают все числа на диагоналях куба (в одном случае образуют два числа, в сумме число 13, в другом 21), а все плоскости, имеющие 4 угла (числа) как внутренние.
На основе теоретического анализа квадратов Кхаджурахо, Дюрера и им подобных квадратов 4×4 выявлены особенности их «строения»: структурные инварианты пандиагональных квадратов 4×4 представляют собой пары чисел, равные в сумме одному из двух чисел Фибоначчи. Числа: 13 или 21.
Магический квадрат представляет собой квадратную таблицу размером n × n, заполненную n2 различными числами, так что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Первый уникальный магический квадрат 4×4 был найден в надписи XI века в индийском городе Кхаджурахо. Квадрат 4×4, изображенный на гравюре Альбрехта Дюрера «Меланхолия», считается старейшим в европейском искусстве (1514 г.). Сумма чисел квадрата Дюрера по любой горизонтали, вертикали и диагонали равна 34. Эта сумма встречается также во всех угловых квадратах 2×2, в центральном квадрате, в квадрате угловых ячеек, на квадратах, построенных по » ход конем» (2+12+15+5 и 3+8+14+9.
Рисунок 1 – Магические квадраты: слева – Гравюра А. Дюрера «Меланхолия»; вверху справа — площадь Дюрера; внизу справа — площадь Кхаджурахо
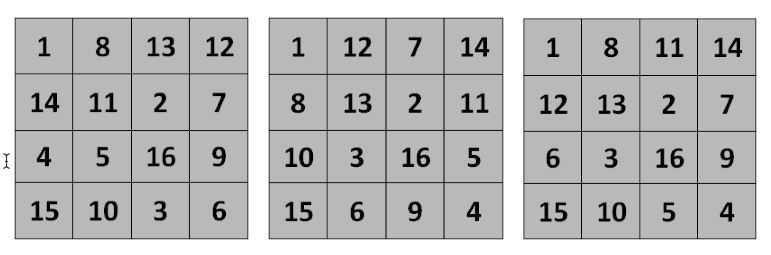
Есть 48 пандиагональных квадратов 4×4 с учетом поворотов и отражений. Если еще учесть симметрию по отношению к торическим параллельным переносам, то остается всего 3 принципиально различных квадрата (рис. 2).
Рисунок 2 – Магические квадраты. Три варианта квадратов (универсальный правый)
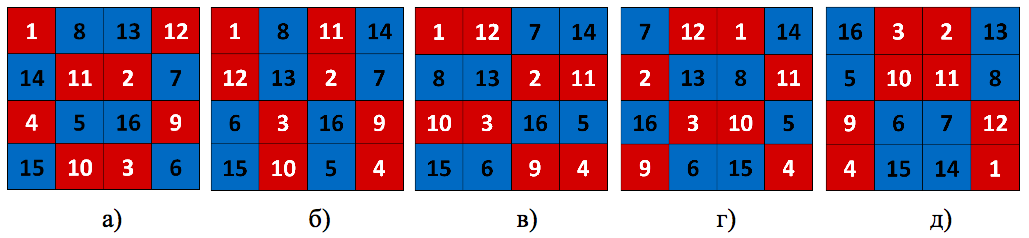
Я проанализировал «структуру» пандиагональных квадратов 4×4 и определил инвариантные части их структуры (рис. 3). Инвариантами структуры пандиагональных квадратов 4×4 являются пары чисел, равные в сумме одному из двух чисел Фибоначчи: 13 или 21. Различные варианты симметричного сочетания этих пар чисел образуют набор квадратов 4×4 пандиагонали.
Рисунок 3 – Магические квадраты: а, б, в – основные варианты квадратов 4×4; г — площадь Кхаджурахо; д — площадь Дюрера
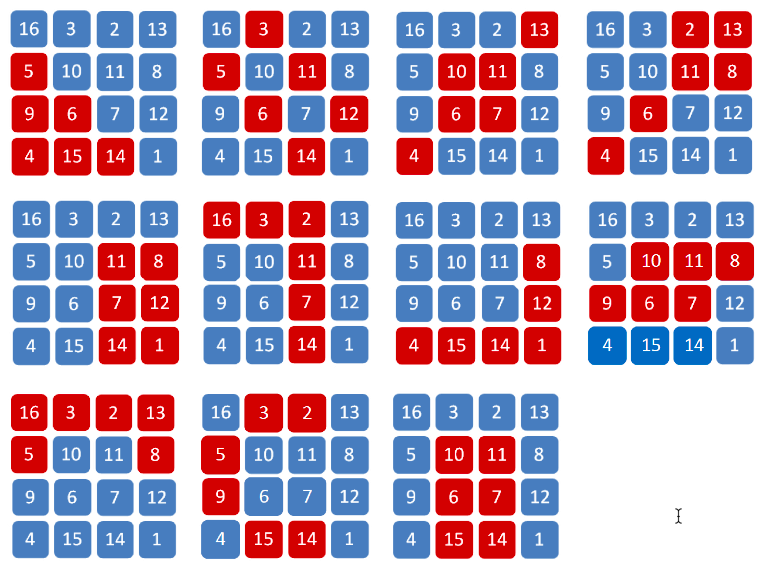
Квадрат Дюрера (и аналогичные четырехугольные квадраты 4×4) имеют симметрию золотого сечения. Например, на рисунке 4 красным и синим квадратами показаны варианты симметрии, где среднее арифметическое суммы красных составляющих квадратов в возможных положениях (4 или 2, когда они вращаются в разные стороны) равно 51. Таким образом, , сумма всех чисел в квадрате равна 136, из них 85 синих, 51 красных. 136/85=1,6; 85/51=1,667.
Рисунок 4 – Магические квадраты. Варианты симметрии на основе квадрата Дюрера
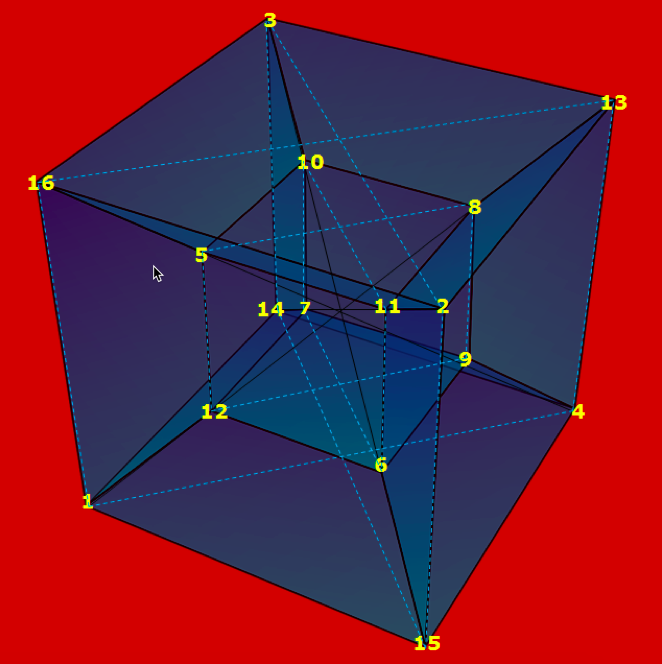
На основе квадрата Дюрера построена геометрическая фигура «куб в кубе», обладающая свойствами симметрии пандиагональных квадратов 4 × 4 (рис. 5). Такое «преобразование» стало возможным, когда вертикальные столбцы квадратных чисел Дюрера располагались под определенным углом, образуя таким образом куб внутри куба. При этом все числа на диагоналях куба обладают свойствами «золотой симметрии» (в одном случае образуются два числа, в сумме число 13, в другом — 21), а все плоскости, имеющие 4 углы (числа) внутреннего и внешнего квадратов построенной фигуры в сумме дают число Фибоначчи 34.
Рисунок 5 – Геометрическая фигура «куб в кубе»
Заключение
- На основе теоретического анализа пандиагональных квадратов 4×4 показаны их «структурные» характеристики: структурными инвариантами пандиагональных квадратов 4×4 являются пары чисел, равные в сумме одному из двух чисел Фибоначчи: 13 или 21.
- Выявлено, что любой вариант шестизначного множества квадрата Дюрера и ему подобных пандиагональных квадратов 4×4, образующих непрерывную симметричную конфигурацию, равен целому числу: 51.
- Строится геометрическая фигура «куб в кубе», обладающая свойствами «золотой симметрии» пандиагональных квадратов 4 × 4. Все числа диагоналей куба обладают свойствами «золотой симметрии» (в одном случае образуются два числа, в сумме число 13, в другом — 21), а все плоскости, имеющие по 4 угла (числа) обоих внутренний и внешний квадраты формы геометрической фигуры в сумме числа Фибоначчи равны 34.
